Латинский квадрат: мистицизм, криптография и «Судоку»

Глава отдела разработки Elbrus Bootcamp Олег Смирнов рассказывает историю латинского квадрата, разбирает агоритмы для его реализации и показывает способ его построения на примере собственного проекта — игры футошики.
Прежде, чем начать, отметим — эта статья не связана напрямую с обучением. Ее задача — расширить кругозор и дать представление о построении матриц разной степени сложности.
Латинский квадрат — это математическая матрица размером n x n. Каждая ее строка и каждый столбец содержат все числа от 1 до n, где от n зависит размер таблицы. Это выглядит так:
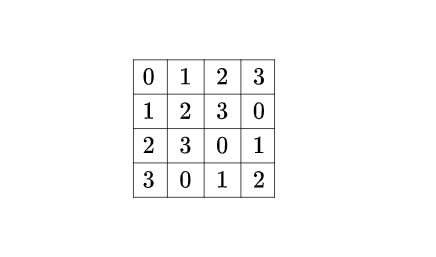
Краткая история латинских квадратов
Первые находки латинских квадратов датируются X-XI веками нашей эры (некоторые исследователи упоминают и более ранние, относящиеся к I веку нашей эры). Вплоть до 18 века они использовались для магических ритуалов — считалось, что амулеты с ними защищают от темных сил и помогают изгнать духов. Сами квадраты тогда назывались магическими.

Магические квадраты, в отличие от латинских, могут быть построены только для чисел и требуют, чтобы сумма всех элементов совпадала в каждой строке и столбце и на диагоналях, а сами числа не повторялись во всем квадрате. В латинских же квадратах набор чисел в каждой строке и столбце одинаковый, меняется только их порядок.
В 1725 году математик Леонард Эйлер использовал для построения квадратов не только цифры, но и буквы латинского алфавита. Отсюда латинские квадраты получили свое название.
Применение
Сейчас латинские квадраты используются в криптографии, протоколах шифрования, в расчетах, которые предваряют научные исследования, и в других областях. Например, в протоколе потокового шифрования Edon80 используется связка из 80 специально отобранных латинских квадратов. Кроме того, матрица применяется в схемах разделения секрета.
Латинские квадраты используются и в играх: например, поле «Судоку» — классический пример реализации такой матрицы. Рассмотрим реализацию матрицы на примере пет-проекта главного разработчика Elbrus Bootcamp Олега Смирнова — игры футошики.
Реализации
Метод Косельни
Один из способов сгенерировать латинский квадрат на несколько десятков ячеек — объединить две другие, меньшие по размеру матрицы. У метода Косельни есть преимущество в виде скорости и сравнительной простоты построения латинского квадрата, но и существенный минус. Получившийся квадрат не будет равномерно распределённым и не подойдет не для криптографии, не для игры — матрицы получаются слишком похожими друг на друга.
У метода есть множество других применений. Его реализацию можно посмотреть здесь.
SeqGen с перегенерацией строки
Хотя этот алгоритм наиболее надежен с точки зрения вероятности распределения каждой цифры в каждую ячейку, он очень медленный. Чем больше квадрат, тем дольше придется ждать результатов генерации, — а при размере более 200 ее можно не дождаться вовсе.
Реализацию метода можно посмотреть здесь.
SeqGen с графом замен
Компромисс между двумя предыдущими вариантами. С одной стороны, алгоритм равномерно распределяет значения только на больших квадратах (от 256 и более), с другой — генерирует их за вполне приемлемое время.
Реализацию метода можно посмотреть здесь.
Метод Джейкобсона и Мэтьюза
Оптимальный подход, если вам нужно достичь баланса между равномерностью распределения символов и алгоритмической сложность. С одной стороны, он позволяет сгенерировать квадрат хорошего качества, с другой — сделать это за строго определенное время.
Реализацию метода можно посмотреть здесь.
Разбор алгоритма Джейкобсона и Мэтьюза
Хотя для генерации небольших квадратов сторонами 100 на 100, которая необходима для реализации футошики, достаточно SeqGen с перегенерацией строки, для примера возьмем метод Джейкобсона и Мэтьюза.
У этого алгоритма несколько преимуществ: он достаточно быстрый и дает очень близкое к равномерному распределение. Кроме того, он весьма интересен в реализации: в отличие от трех предыдущих, он рассматривает латинский квадрат не как матрицу, а как трехмерный куб.
Это альтернативное представление квадрата, в котором каждая ось соответствует его строкам, колонкам и символам. Каждая ячейка трехмерного куба содержит 1, если на пересечении строки и колонки находится символ. В ином случае ячейка содержит 0.
Шаг алгоритма
Шагом алгоритма мы будем называть добавление и вычитание единицы в некоторых ячейках куба таким образом, чтобы не изменять сумму элементов в каждой строке по всем трем осям куба. Эта сумма всегда должна быть равна 1. В процессе хода может образоваться ячейка, содержащая значение -1. Так как сумма строки обязана быть неизменной, в строке со значением -1 будет присутствовать две ячейки со значением 1.
Куб, содержащий ячейку со значением -1, будет считаться незаконченным.
Шаги делятся на два типа: из законченного куба и из незаконченного куба.
- Для шага из законченного куба выбираем любую ячейку со значением 0, а затем называем ее t и определяем координаты как (t.x, t.y, t.z). Эта ячейка связана с тремя строками в кубе, каждая из которых параллельна одной из осей и в каждой из которых находится только одна ячейка со значением 1. Назовем координаты таких ячеек (x1, y1 и z1) и получим подкуб размером 2x2x2. Он не обязательно будет состоять из соседних клеток, а шагом будет считаться добавление 1 к (t.x, t.y, t.z) и вычитание таким образом, чтобы в каждой строке по каждой оси сумма всех ячеек осталась равной. Если после совершения шага противоположная ячейка c координатами содержит значение -1, то получившийся куб считается незаконченным. В ином случае куб законченный.
- Для шага из незаконченного куба алгоритм вычитания и добавления остаётся прежним, но меняется алгоритм вычисления t и координат (x1, y1 и z1). В качестве значения t мы берём ячейку со значением -1. Такая ячейка в кубе может быть только одна. В строке x , соответствующей координате t.x, находится одна ячейка со значением -1 и две ячейки со значением 1. В качестве x1, y1 и z1 выбираем любую из этих двух ячеек.После этого хода мы точно так же можем получить как законченный, так и незаконченный куб.
Джейкобсон и Мэтьюз доказали, что любые два куба инцидентности связаны между собой конечным числом шагов. Таким образом, для генерации куба нужно соблюсти три условия:
- для всех случайных значений нужно использовать качественный генератор случайных чисел;
- необходимо повторить шаг алгоритма как минимум раз;
- только законченный куб можно преобразовать в корректный латинский квадрат.
Наивная реализация на JavaScript
Реализация, которую можно посмотреть здесь, неэффективна, зато лего читаема. Код написан на JavaScript, визуализация — на React и Three.js.
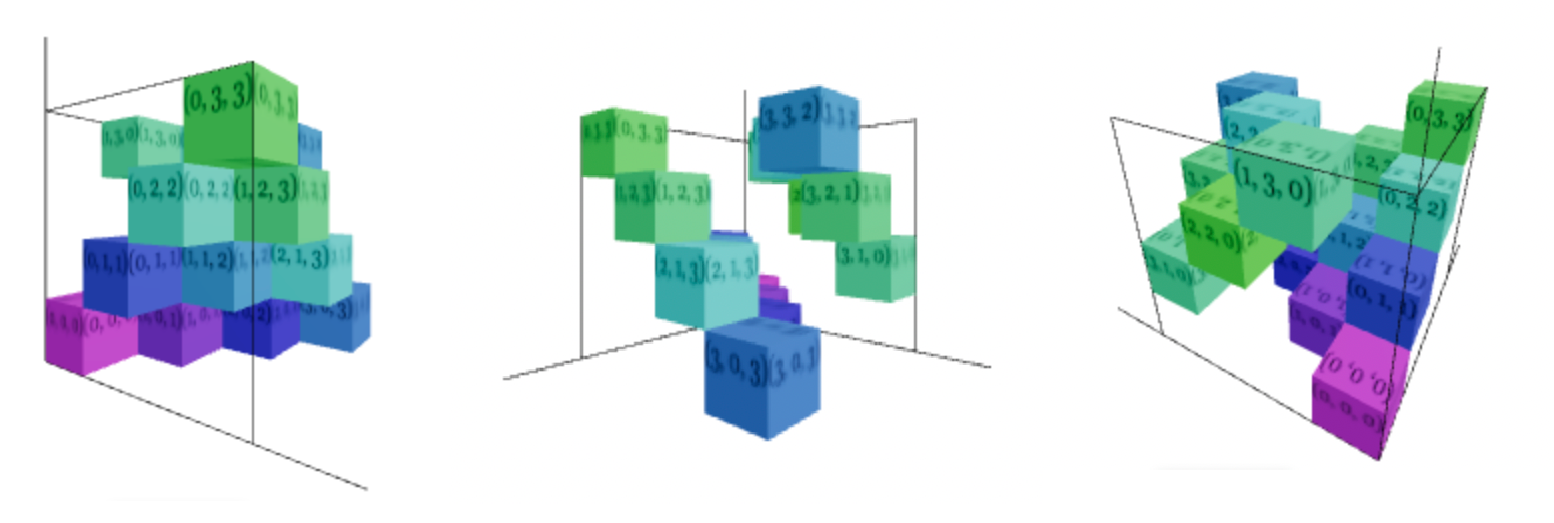
Вращать куб по осям можно с помощью полосок-слайдеров, а запускать алгоритм — кнопками Step (пошагово) и Shuffle (целиком). Соответствующий кубу латинский квадрат отображается справа.



